1Learning Outcomes¶
Understand how the normalized number representation in the IEEE 754 single-precision floating point standard is inspired by scientific notation.
Identify how the IEEE 754 single-precision floating point format uses three fields:
The sign bit represents sign
The exponent field represents the exponent value.
The significand field represents the fractional part of the mantissa value.
For normalized numbers:
The exponent field represents the exponent value as a bias-encoded number
The mantissa always has an implicit, leading one.
🎥 Lecture Video
Omitted (for the purposes of the next section): Overflow and Underflow, 6:54 - 8:40
2Intuition: Scientific Notation¶
Instead of identifying the fixed binary point location across every number in our representation, the floating point paradigm determines a binary point location for each number.
Consider the decimal number 0.1640625 which has binary representation[1]
There are many zeros in this binary representation. For example, there is no integer component, so everything to the left of the binary point is zero. In fact, there are really only one “interesting” range with some “energy”, e.g., varying ones and zeros: 10101. This bit pattern is located two values right of the binary point.
With these two pieces of information—what the significant bits are, and what exponent the significant bits are associated with—we can suddently represent both very large and very small numbers. This is the intuition behind scientific notation.
2.1Scientific Notation (Base-10)¶
You may have seen scientific notation in a physics or chemistry course, but we review it here and introduce core terminology that carry over into the binary case. The scientific notation for the number 0.1640625 is (Figure 1):
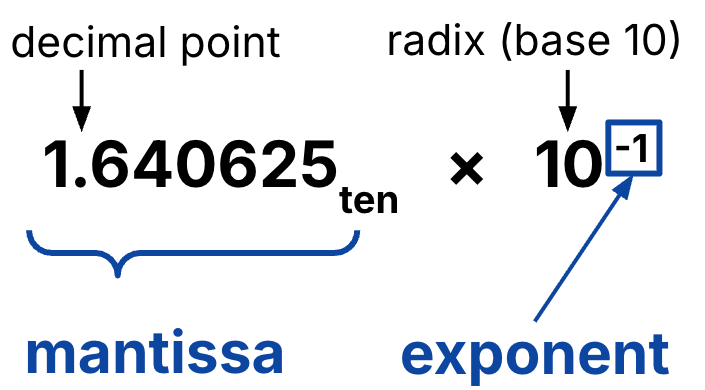
Figure 1:Scientific notation assumes a normalized form, where the mantissa has exactly one non-zero digit to the left of the decimal point.
Radix: The base. In decimal, base 10.
Mantissa: The “energy” of the number, i.e., the significant figures (1.640625 in Figure 1)
Exponent: The power the radix is raised to (-1 in Figure 1).
Scientific notation assumes a normalized form of numbers, where the mantissa has exactly one digit to the left of the decimal point.
Every number represented in scientific notation has exactly one normalized form for a given number of significant figures. For example, the number has normalized form (for two significant figures) and non-normalized forms , and so on.
2.2Binary Normalized Form¶
The number 0.1640625 in a binary normalized form is (Figure 2):
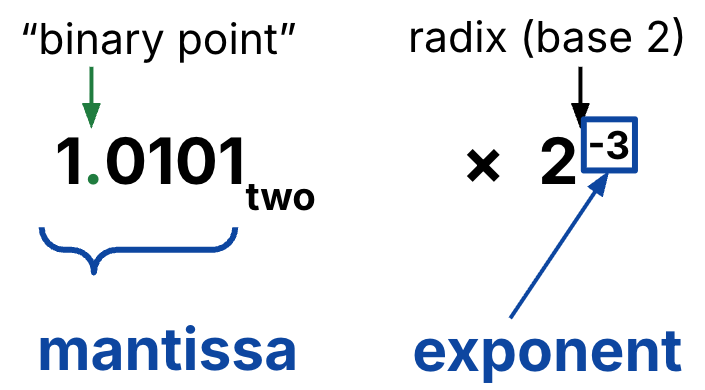
Figure 2:In binary, we also assume a normalized form, where the mantissa has exactly one non-zero digit to the left of the binary point.
We close this discussion with two important points:
A 32-bit floating point representation of binary normalized form should allocate two separate fields within the 32 bits—one to represent the mantissa, and one to represent the exponent.
With binary normalized form, mantissa always have a leading one.
Binary normalized form means mantissa is always of the form 1.xyz...!
1.xyz...!Why? Consider the definition of normalized form:
The mantissa has exactly one non-zero digit to the left of the decimal point.
In binary, there is only one non-zero digit: 1. This means that a representation like is not normalized and must be scaled down by a power of 2 to its normalized form, .
3IEEE 754 Single-Precision Floating Point¶
This discussion leads us to the definition of the IEEE 754 Single-Precision Floating Point, which is used for the C float variable type. This format leverages binary normalized form to represent a wide range of numbers for scientific use using 32 bits.[2]
This standard was pioneered by UC Berkeley Professor William (“Velvel”) Kahan. Prior to Kahan’s system, the ecosystem for representing floating points was chaotic, and calculations on one machine would give different answers on another. By leading the effort to centralize floating point arithmetic into the IEEE 754 standard, Professor Kahan earned the Turing Award in 1988.
The three fields in the IEEE 754 standard are designed to maximize the accuracy of representing many numbers using the same limited precision of 32 bits (for single-precision, and 64 bits for double-precision). This leads us to two important definitions to help us quantify the efficacy of this number representation:
Precision is a count of the number of bits used to represent a value.
Accuracy is the difference between the actual value of a number and its computer representation.
Without further ado, Figure 3 defines the three fields in the IEEE 754 single-precision floating point for 32 bits.

Figure 3:Bit fields in IEEE 754 single-precision floating point. The least significant bit (rightmost) is indexed 0; the most significant bit (leftmost) is indexed 31.
4Normalized Numbers¶
The three fields in Figure 3 can be used to represent normalized numbers of the form in Equation (1).
This design will seem esoteric at first glance. Why is there a ? Where did the mantissa go—what’s a significand? Why is the exponent offset by -127? As stated before, these three fields are defined to maximize the accuracy of representable numbers in 32 bits. In other words, none of the bit patterns in these three fields use two’s complement! Instead, the standard uses Table 1 defines precisely how to interpret each field’s bit pattern for representing normalized numbers.
Table 1:Sign, exponent, and significand fields for normalized numbers.
| Field Name | Represents | Normalized Numbers[3] |
|---|---|---|
| s | Sign | 1 is negative; 0 is positive |
| exponent | Bias-Encoded Exponent | Subtract 127 from exponent field to get the exponent value. |
| significand | Fractional Component of the Mantissa | Interpret the significand as a 23-bit fraction (0.xx...xx) and add 1 to get the mantissa value. |
Why use bias-encoded exponents?
Designers wanted floating point numbers to be supported even when specialized floating point hardware didn’t exist. For example, it should still be possible to sort floating point numbers using just integer compares, as long as we know which bit fields should be considered.
To support sorting numbers of the same sign with just integer hardware, a bigger exponent field should represent bigger numbers. With two’s complement, negative numbers would look bigger (because they lead with 1, the sign-bit). With bias encoding, on the other hand, all floating point numbers are ordered by the value of the exponent: the 000...000 exponent field represents the smallest exponent value (numbers are ), and the 111....111 exponent field represents the largest exponent value (numbers are ).
Why not directly represent mantissa? Why assume an implicit 1?
Remember that in binary normalized form, the mantissa always leads with a 1. IEEE 754 represents normalized numbers by assuming that there is always an implicit 1, then having the significand explicitly representing the bits bits after the binary point. In other words, it is always true that for normalized numbers, 0 < significand < 1.
This assumption for normalized numbers helps IEEE 754 single-precision pack more representable (normalized) numbers into the same 23 bits, because now we represent 24-bit (normalized) mantissas! In other words, the precision is 24 bits, though we only 23 bits.
5Zero, Infinity, and More¶
Normalized numbers are not the only values that can be represented by the IEEE 754 standard. We discuss zero, infinity, and other numbers in a later section.
5.1IEEE 754 Double-Precision Floating Point¶
The IEEE 754 double-precision floating point standard is used for the C double variable type. It has three fields, now over 64 bits:
Sign: Still 1 sign bit (most significant bit, bit index 63)
Exponent: 11 bits with bias -1023
Significand: now 52 bits
The primary advantage is greater accuracy due to the larger significand. The normalized form can represent numbers from about to .
6Use a Floating Point Converter¶
Check out this web app for a simple converter between decimal numbers and their IEEE 754 single-precision floating point format.
While we would love for you to use the converter to understand the comic in Figure 4, it should be noted that the robot is assuming IEEE 754 double-precision format (see another section).

Figure 4:Welcome to the Secret Robot Internet (SMBC Comics).
Because floating point is based on powers of two, it cannot represent most decimal fractions exactly. Here, 0.3 is inaccurately represented as 0.29999999999, and with doubles is 0.30000000000000004. Read more about doubles, addition, and accuracy in another section.
We leave this conversion as an exercise to the reader.
The IEEE 754 Double-Precision Floating Point is used for the C
doublevariable type, which is 64 bits. Read more in a bonus section.Only valid when exponent field is in the range
0000001(1) to1111110(254), i.e., when it is neither 0 nor 255.